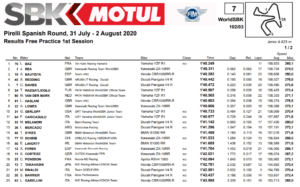
Ad accogliere i piloti sulla pista di Jerez per la ripartenze del Campionato SBK c’è il loro nemico numero uno: il caldo. Chi riesce a gestire meglio le alte temperature è Loris Baz, che conclude il venerdì in cima alla classifica dei tempi, dopo essere stato il migliore in FP1; alle sue spalle Rea e Rinaldi.

27 sono i gradi che si trovano a combattere i piloti a Jerez, che diventano 36 sull’asfalto… al mattino. A complicare tutto, un tasso di umidità elevatissimo rende luglio decisamente il periodo non ideale per correre in questa zona della Spagna. Ma i piloti non vedono l’ora di tornare in pista (come biasimarli!), nonostante i tempi si mantengano abbastanza “tranquilli”, con Loris Baz che nelle FP1 segna un 1’40.249. Attaccato a lui, con soli 6 centesimi di ritardo, troviamo Rea, mentre sono staccati di 0.143 e 0.193 rispettivamente Bautista e Redding, con il primo che è il padrone di casa e il secondo che ha testato e girato molte volte all’Angel Nieto, grazie anche alla sua permanenza in MotoGP.
A 3 centesimi dal ducatista troviamo il suo compagno di squadra, Davies, seguito dalle Yamaha di Razgatlioglu e van der Mark. Chiudono la top ten Haslam (+0.354), Lowes (+0.357) e Gerloff (+0.484). Chiude ventunesimo su 23, Micheal Rinaldi, dopo una caduta ad alta velocità alla curva 6.
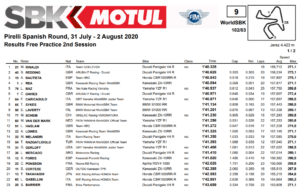
Nelle FP2 sono in pochi a migliorare i propri tempi, complici anche le temperature che continuano ad alzarsi (34°C aria, 40°C asfalto). Aggiorna il proprio crono Michael Rinaldi, dopo il giro nella ghiaia in mattinata, fermandosi su un 1’40.325 che gli vale la testa della classifica dei tempi pomeridiana e un terzo posto a fine giornata di libere. Lo seguono a 3 decimi Scott Redding, Bautista (+0.518) e Rea (+0.569). Loris Baz si prende la quinta piazza, precedendo Davies e Caricasulo, i quali chiudono con un tempo fotocopia di 1’40.971, a 6 decimi da Rinaldi. Anche Sykes, Laverty e Scheib riescono a migliorarsi dal mattino, chiudendo la top ten del pomeriggio spagnolo.
Cadute innocue per Chaz Davies ed Eugene Laverty, usciti rispettivamente in curva 2 e 1.